Further details & calculation on Standard Deviation

Standard Deviation and Variance

Deviation just means how far from the normal

Standard Deviation

The Standard Deviation is a measure of how spread out numbers are.
Its symbol is σ (the greek letter sigma)
The formula is easy: it is the square root of the Variance. So now you ask, "What is the Variance?"

Variance

The Variance is defined as:

The average of the squared differences from the Mean.

To calculate the variance follow these steps:

Work out the Mean (the simple average of the numbers)
Then for each number: subtract the Mean and square the result (the squared difference).
Then work out the average of those squared differences. (Why Square?)

Example

You and your friends have just measured the heights of your dogs (in millimeters):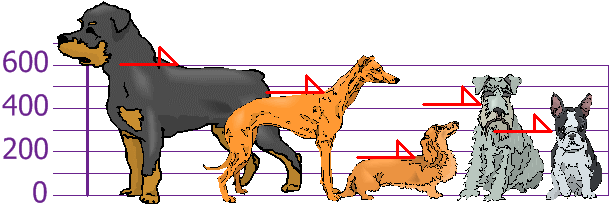

The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:

Answer:

Mean =	600 + 470 + 170 + 430 + 300	=	1970	= 394
	5		5

so the mean (average) height is 394 mm. Let's plot this on the chart:

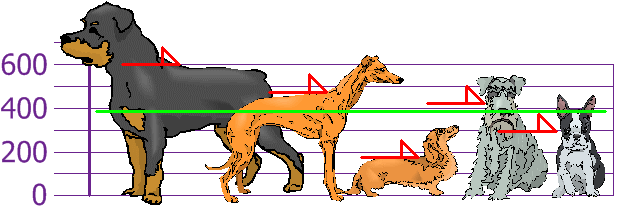
Now, we calculate each dogs difference from the Mean:

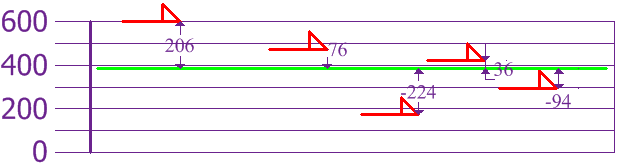
To calculate the Variance, take each difference, square it, and then average the result:

Variance: σ2 =	2062 + 762 + (-224)2 + 362 + (-94)2	=	108,520	= 21,704
	5		5

So, the Variance is 21,704.
And the Standard Deviation is just the square root of Variance, so:

Standard Deviation: σ = √21,704 = 147.32... = 147 (to the nearest mm)

And the good thing about the Standard Deviation is that it is useful. Now we can show which heights are within one Standard Deviation (147mm) of the Mean:

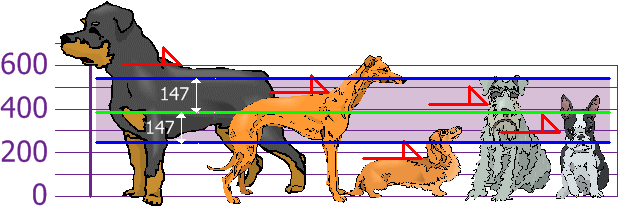
So, using the Standard Deviation we have a "standard" way of knowing what is normal, and what is extra large or extra small.
Rottweillers are tall dogs. And Dachsunds are a bit short ... but don't tell them!

Now try the Standard Deviation Calculator.

The Formulas

We have just been using this formula: (The "Population Standard Deviation")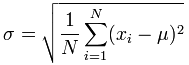
And there is also this formula: (The "Sample Standard Deviation")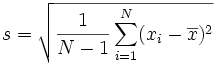

They are both explained at Standard Deviation Formulas if you want to know more.

*Note: Why square ?

Squaring each difference makes them all positive numbers (to avoid negatives reducing the Variance)
And it also makes the bigger differences stand out. For example 100²=10,000 is a lot bigger than 50²=2,500.
But squaring them makes the final answer really big, and so un-squaring the Variance (by taking the square root) makes the Standard Deviation a much more useful number.

(reference taken from mathisfun)

NB: Having explained in details for the above, if you still do not understand how standard deviation is derived, just to reassure you that it is perfectly fine. The above detail information is only useful for those who are extremely curious about how standard deviation is calculated.

How PSLE Aggregate and T-Scores are calculated?

To understand how PSLE Aggregate Scores are calculated, we must first understand T-Score. T-Score is the adjusted score a student will get for a subject, after a series of tabulations has been made.

Formula for T-Score

X = Raw score of student
Y = Average Score of the whole cohort
Z = Standard Deviation* (SD)

Standard Deviation* (SD) is the spread of the marks around the average.

Example 1 -
Allan, Bernard and Charles have $45, $50 and $55 respectively. They have an average of $50 each.

Example 2 -
Dan, Edward and Frank have $10, $50 and $90 respectively. They also have an average of $50 each.

In Example 1, the spread ($45 to average of $50 and $55 to average of $50) is smaller than the spread in Example 2, where the spread is bigger ($10 to average of $50 and $90 to average of $50)

As such, Example 1 will have a smaller SD, as compared to Example 2.

A more detailed explanation of how SD is calculated can be found in next page under Standard deviation cal.


Simpler Way to read Standard Deviation (SD)
If the average score of 3000 pupils who sat for Science Test is 50 marks and the SD is 5, it means that 2/3 of the 3000 pupils have scored 5 marks around the average, which means 2000 of the students scored from 45 to 55 marks.

If the average score of the same 3000 pupils who sat for Mathematics Test is 50 marks and the SD is now 10, it means that 2/3 of the 3000 pupils have scored 10 marks around the average, which means 2000 students scored from 40 to 60 marks.


Example of how T-score is calculated
Li Ting’s score for Mathematics – 90 (X)
Average score of cohort – 75 (Y)
Standard Deviation - 20 (Z) (this means 2/3 of cohort scored from 55 to 95)

Using the T-Score formula

T = 50 + 10(X – Y) / Z

T = 50 + 10 x (90 – 75) / 20

= 50 + 10 x 15/20

= 50 + 10 x 0.75

= 57.5

Li Ting’s T-score for Mathematics is 57.5
Now that we have covered T-score, we can take a look at PSLE Aggregate Score.


Using T-Score to Calculate PSLE Aggregate Score
Let’s now take a look at Li Ting’s total performance



The cohort’s average and standard deviation plays a big part in Li Ting’s score. To demonstrate, let’s move the average scores of all subjects down by 10 marks each, keeping all other variables (raw score and SD) constant. This is how Li Ting’s score will now look like.




Take note that Li Ting’s aggregate goes up from 245 to 260 when the averages of all subjects went down by 10 marks each. This shows that if the cohort is weaker, Li Ting’s aggregate score will increase, even if she scores the same marks for all the subjects.

It is therefore not accurate to compare a student’s aggregate score in a particular year, to the aggregate score of another student in a different year. Each year will have a different average for all the subjects.

Parents who have more than 1 child, tend to compare each child’s PSLE Aggregate Score with his/her sibling's score. This is not a very fair comparison.


Final Note –

Because PSLE aggregate score is based on T-scores, theoretically, there is no such thing as “maximum aggregate score”.

Many parents believe the (non-existent) maximum aggregate is 300. That is a misconception.

To demonstrate, I have bumped up Li Ting’s score (in Table 3) to full marks for all her subjects, using the same averages and SDs found in Table 2.




Note that although Li Ting scored 100% marks for all subjects, her PSLE Aggregate Score is only 286. She did not score the (imaginary and non-existent maximum) PSLE Aggregate Score of 300!

The only way to score that 300 (or even above that), is to have a very weak cohort in your year.


So if our imaginary Li Ting scored 100% for all her subjects and still only scored 286 for her PSLE Aggregate, how did Ms Natasha score a PSLE Aggregate of 294 for the year 2007? I don’t have the stats, but my guess is that the averages and SDs of the individual subjects of the cohort played a big role.

In any case, 294 is a respectable score, and we should give credit where it is due. It is an all time high and Ms Natasha definitely deserves the recognition for her outstanding performance.

I hope the article in this post gives parents and students a better picture how PSLE Aggregate Scores are calculated
(with reference taken from excel eduervice)