Further details & calculation on Standard Deviation

Standard Deviation and Variance

Deviation just means how far from the normal

Standard Deviation

The Standard Deviation is a measure of how spread out numbers are.
Its symbol is σ (the greek letter sigma)
The formula is easy: it is the square root of the Variance. So now you ask, "What is the Variance?"

Variance

The Variance is defined as:

The average of the squared differences from the Mean.

To calculate the variance follow these steps:

Work out the Mean (the simple average of the numbers)
Then for each number: subtract the Mean and square the result (the squared difference).
Then work out the average of those squared differences. (Why Square?)

Example

You and your friends have just measured the heights of your dogs (in millimeters):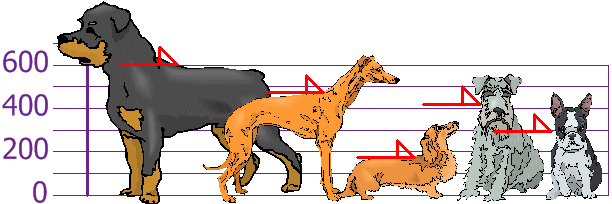

The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:

Answer:

Mean =	600 + 470 + 170 + 430 + 300	=	1970	= 394
	5		5

so the mean (average) height is 394 mm. Let's plot this on the chart:

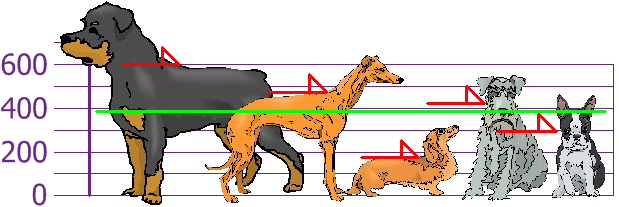
Now, we calculate each dogs difference from the Mean:

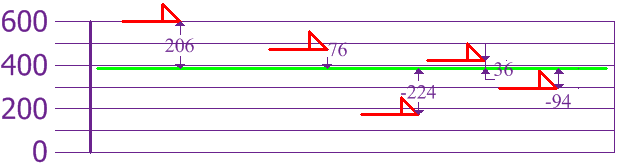
To calculate the Variance, take each difference, square it, and then average the result:

Variance: σ2 =	2062 + 762 + (-224)2 + 362 + (-94)2	=	108,520	= 21,704
	5		5

So, the Variance is 21,704.
And the Standard Deviation is just the square root of Variance, so:

Standard Deviation: σ = √21,704 = 147.32... = 147 (to the nearest mm)

And the good thing about the Standard Deviation is that it is useful. Now we can show which heights are within one Standard Deviation (147mm) of the Mean:

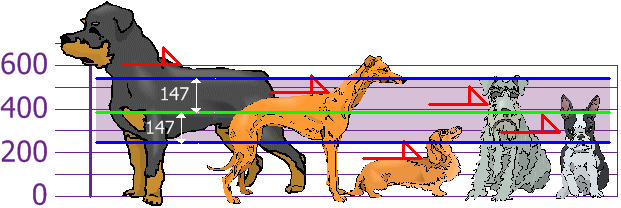
So, using the Standard Deviation we have a "standard" way of knowing what is normal, and what is extra large or extra small.
Rottweillers are tall dogs. And Dachsunds are a bit short ... but don't tell them!

Now try the Standard Deviation Calculator.

The Formulas

We have just been using this formula: (The "Population Standard Deviation")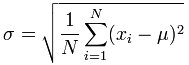
And there is also this formula: (The "Sample Standard Deviation")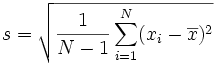

They are both explained at Standard Deviation Formulas if you want to know more.

*Note: Why square ?

Squaring each difference makes them all positive numbers (to avoid negatives reducing the Variance)
And it also makes the bigger differences stand out. For example 100²=10,000 is a lot bigger than 50²=2,500.
But squaring them makes the final answer really big, and so un-squaring the Variance (by taking the square root) makes the Standard Deviation a much more useful number.

(reference taken from mathisfun)

NB: Having explained in details for the above, if you still do not understand how standard deviation is derived, just to reassure you that it is perfectly fine. The above detail information is only useful for those who are extremely curious about how standard deviation is calculated.